Réseaux de Bravais

En cristallographie, les réseaux de Bravais, au nombre de 14, représentent une façon mathématique (géométrie dans l'espace) de classifier les différents types de cristaux. La symétrie d'un cristal peut être inférieure à celle de sa maille primitive dans le cas où les groupes d'atomes situés aux sommets de la maille ne présentent pas la même symétrie que la maille.

Chaque système, ou réseau élémentaire, peut se décliner de quatre manières :

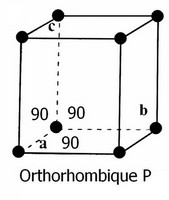
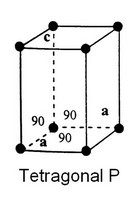
primitive (notée P) : il y a une particule (ou motif) à chaque sommet
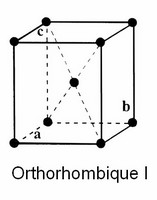
centrée (notée I, de l'allemand innenzentriert) : il y a en plus une particule au centre de la maille
à faces centrées (notée F) : il y a en plus une particule au centre de chaque face
à deux faces centrées (notée A, B ou C suivant l'axe concerné) : il y a une particule au centre de deux faces opposées
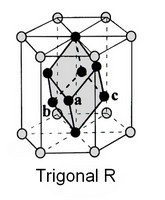
La forme primitive du système rhomboédrique peut également être notée R.

Tous les systèmes possèdent une forme primitive P, mais pas obligatoirement toutes les autres formes dérivées. Voici la liste des réseaux acceptés par chaque systèmes :

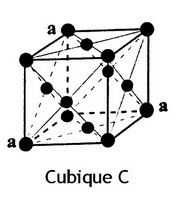
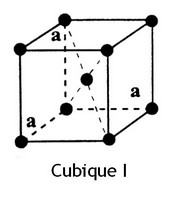
cubique : P, I et F (3 réseaux)
quadratique : P, I (2 réseaux)
orthorhombique : P, I, F, A (ou B ou C) (4 réseaux)
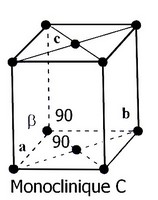
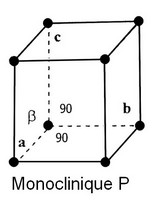
monoclinique : P, A (si a ¹ 90°) (2 réseaux)
triclinique : P (1 réseau)
rhomboédrique : P (ou R) (1 réseau)
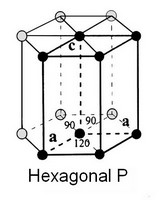
hexagonal : P (1 réseau)

On a bien un total de quatorze réseaux de Bravais, les voila représentés dans les 7 systèmes cristallins :