Systèmes cristallins : Différence entre versions
| Ligne 67 : | Ligne 67 : | ||
{| align="center" class="toccolours" cellspacing="0" | {| align="center" class="toccolours" cellspacing="0" | ||
|- bgcolor="#ccccff" | |- bgcolor="#ccccff" | ||
| − | | align="center" | '''[[ | + | | align="center" | '''[[à voir aussi pour tout ce qui concerne les cristaux]]''' |
|- | |- | ||
| align="center" style="font-size: 100%;" | | | align="center" style="font-size: 100%;" | | ||
[[Les macles]] | [[Cristal]] | [[La cristallographie]] | [[Troncatures]] | [[Les macles]] | [[Cristal]] | [[La cristallographie]] | [[Troncatures]] | ||
|} | |} | ||
Version du 2 mai 2009 à 13:28
Sommaire
systèmes cristallins
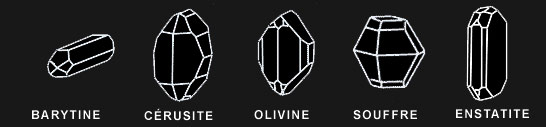
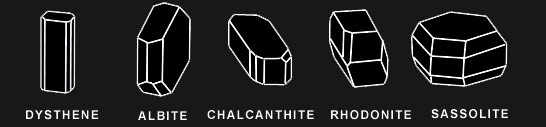
Un cristal est un solide polyédrique, à structure régulière et périodique, formée d'un ensemble ordonné d'un grand nombre d'atomes, de molécules ou d'ions.
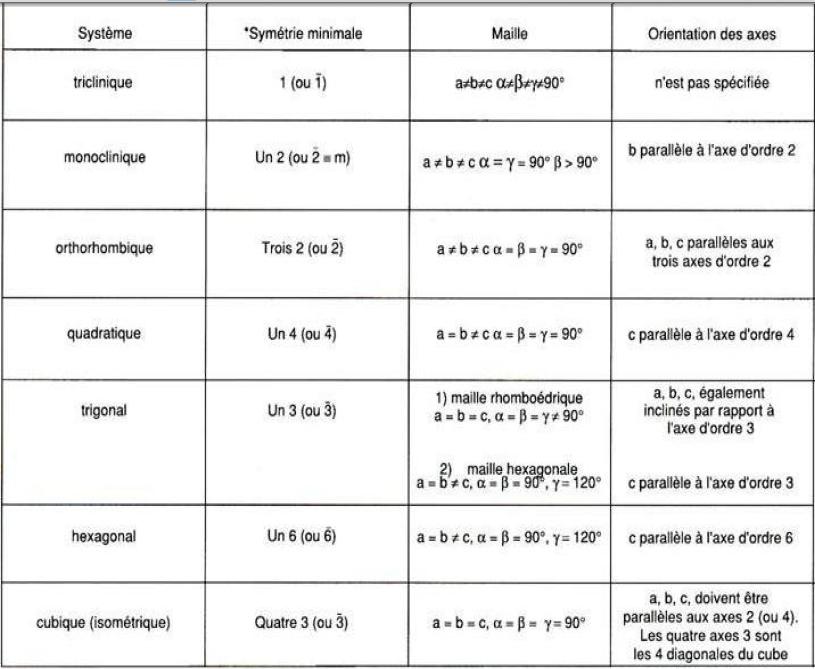
L'étude des cristaux permet de visualiser des plans, axes et centres de symétrie… L'étude des divers éléments de symétrie, a débouché sur la mise en évidence de 14 types de réseaux cristallins (les réseaux " de Bravais "), liés à 7 types fondamentaux de symétrie d'orientation : les 7 systèmes cristallins.
Ces systèmes sont caractérisés par le rapport des longueurs des trois vecteurs "a, b, c," et des trois axes "x, y, z," et des trois angles "α, β, γ," que forment entre eux ces axes. Les indices de Miller sont des coordonnées des vecteurs dans cette base.
Dans l'énumération qui suit, on donne, le nom du système cristallin, la forme de la maille élémentaire, le rapport des 3 axes (a/b/c), celui des 3 angles (alpha/béta/gamma), entre eux…
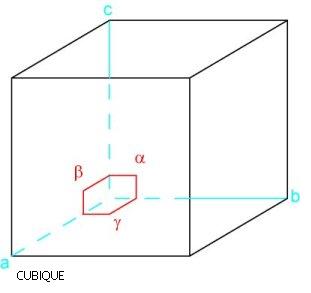
Système cubique
cube ; a = b = c ; alpha = béta = gamma = 90°
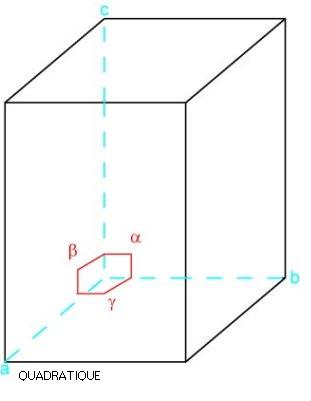
Système quadratique
prisme droit à 4 faces rectangulaires égales et à 2 bases carrées ; a = b ≠ c ; alpha = béta = gamma = 90°
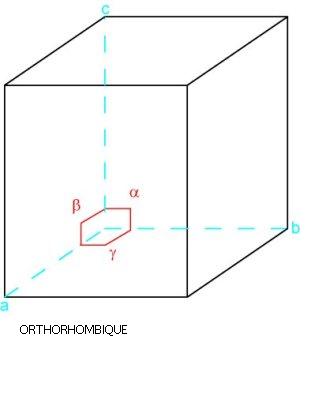
Système orthorhombique
prisme droit à 4 faces rectangulaires égales 2 à 2 et à 2 bases rectangulaires ; a ≠ b ≠ c ; alpha = béta = gamma = 90°
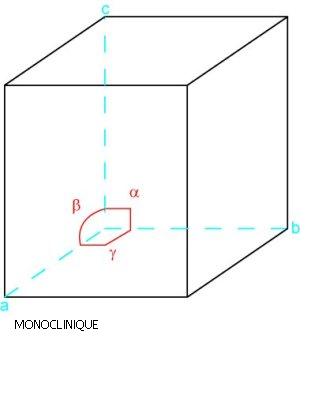
Système monoclinique (ou clinorhombique)
prisme oblique à 4 faces parallélogramatiques égales 2 à 2 et à 2 bases rectangulaires ; a ≠ b ≠ c ; alpha = gamma = 90°, béta ≠ 90°
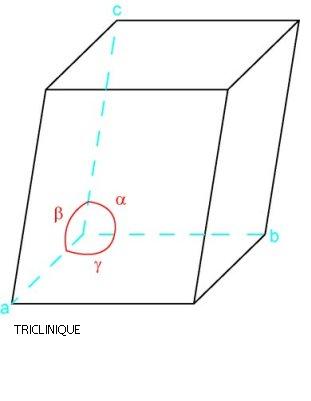
Système triclinique
prisme oblique à 4 faces latérales et à bases parallélogramatiques égales 2 à 2 ; a ≠ b ≠ c ; alpha ≠ béta ≠ gamma, aucun = 90°
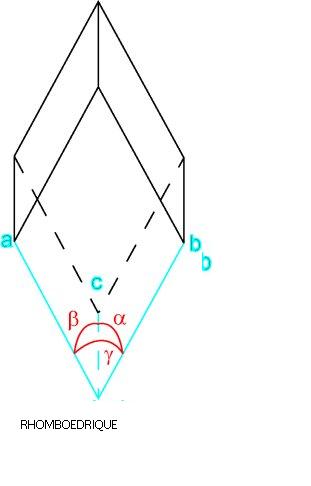
Système trigonal (ou rhomboédrique)
6 faces losangiques égales (rhomboèdre) ; a = b = c ; alpha = béta = gamma ≠ 90°
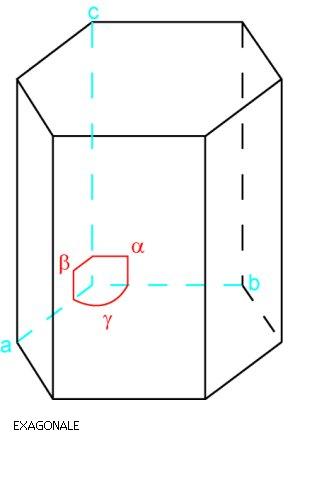
Système hexagonal
prisme droit à 6 faces latérales rectangulaires égales et à 2 bases hexagonales ; a = b ≠ c ; alpha = béta = 90° gamma = 120°
| à voir aussi pour tout ce qui concerne les cristaux |