Forme : Différence entre versions
m |
|||
| Ligne 10 : | Ligne 10 : | ||
Exemple : la forme {111} comprend la face (111) et toutes les faces équivalentes à (111) par symétrie. | Exemple : la forme {111} comprend la face (111) et toutes les faces équivalentes à (111) par symétrie. | ||
| − | Il convient de noter qu'une forme peut | + | Il convient de noter qu'une forme peut : |
| − | *<b>fermée</b>, et constituer à elle seule un cristal (exemple : l'octaèdre de la fluorite, constitué de 8 faces triangulaires) ; | + | * être <b>fermée</b>, et constituer à elle seule un cristal (exemple : l'octaèdre de la fluorite, constitué de 8 faces triangulaires) ; |
| − | **les formes fermées | + | **les formes fermées sont des volumes à elles seules, aucune face ne manque. Exemples : |
***Tétraèdre : forme fermée composée de quatre faces ; | ***Tétraèdre : forme fermée composée de quatre faces ; | ||
***Cube (ou hexaèdre) : forme fermée composée de six faces carrées ; | ***Cube (ou hexaèdre) : forme fermée composée de six faces carrées ; | ||
| Ligne 18 : | Ligne 18 : | ||
***etc. | ***etc. | ||
| − | *<b>ouverte</b>, et doit, pour constituer un cristal, s'additionner à d'autres formes ouvertes (exemple le prisme du quartz, constitué de 6 faces rectangulaires, auquel s'ajoutent les 2 rhomboèdres constituant une bipyramide qui ferment le cristal). | + | * ou <b>ouverte</b>, et doit, pour constituer un cristal, s'additionner à d'autres formes ouvertes (exemple le prisme du quartz, constitué de 6 faces rectangulaires, auquel s'ajoutent les 2 rhomboèdres constituant une bipyramide qui ferment le cristal). |
| − | **les formes ouvertes dont les faces ne peuvent seules | + | **les formes ouvertes - dont les faces ne peuvent pas, à elles seules, former un volume - doivent impérativement s'associer à d'autres formes : |
***Pedion (= monoèdre) : cette forme ouverte est composée d'un seul plan (face) ; | ***Pedion (= monoèdre) : cette forme ouverte est composée d'un seul plan (face) ; | ||
***Pinacoïde : forme ouverte composée de deux plans (faces) parallèles ; | ***Pinacoïde : forme ouverte composée de deux plans (faces) parallèles ; | ||
| Ligne 29 : | Ligne 29 : | ||
Un cristal ne peut donc pas consister en une seule forme ouverte, tandis qu'il peut développer une seule forme fermée (tel le cube illustré ci-dessus). | Un cristal ne peut donc pas consister en une seule forme ouverte, tandis qu'il peut développer une seule forme fermée (tel le cube illustré ci-dessus). | ||
| − | La nomenclature officielle française des formes cristallines fut publiée dans : J.D.H. Donnay et H. Curien, « Nomenclature des 47 formes cristallines ».<br>Classification des 47 | + | La nomenclature officielle française des formes cristallines fut publiée dans : J.D.H. Donnay et H. Curien, « Nomenclature des 47 formes cristallines ».<br>Classification des 47 formes cristallines : |
:Pedion | :Pedion | ||
:Pinacoïde | :Pinacoïde | ||
Version du 26 avril 2011 à 20:41
Une forme cristalline est un ensemble de faces (parfois une face unique), participant à la construction d'un cristal, ces faces sont dans un rapport de symétrie.
Une forme cristalline est caractérisée par :
- -le nombre des faces,
- -la symétrie du cristal,
- -l'orientation de la face originale par rapport aux éléments de symétrie du cristal,
- -sa symétrie propre,
- -son nom officiel.
Une forme est indiquée par les indices d'une de ses faces, de préférence celle qui a les valeurs les plus positives. Les indices d'une forme sont écrits entre accolades.
Exemple : la forme {111} comprend la face (111) et toutes les faces équivalentes à (111) par symétrie.
Il convient de noter qu'une forme peut :
- être fermée, et constituer à elle seule un cristal (exemple : l'octaèdre de la fluorite, constitué de 8 faces triangulaires) ;
- les formes fermées sont des volumes à elles seules, aucune face ne manque. Exemples :
- Tétraèdre : forme fermée composée de quatre faces ;
- Cube (ou hexaèdre) : forme fermée composée de six faces carrées ;
- Octaèdre : forme fermée composée de huit faces triangulaires ;
- etc.
- les formes fermées sont des volumes à elles seules, aucune face ne manque. Exemples :
- ou ouverte, et doit, pour constituer un cristal, s'additionner à d'autres formes ouvertes (exemple le prisme du quartz, constitué de 6 faces rectangulaires, auquel s'ajoutent les 2 rhomboèdres constituant une bipyramide qui ferment le cristal).
- les formes ouvertes - dont les faces ne peuvent pas, à elles seules, former un volume - doivent impérativement s'associer à d'autres formes :
- Pedion (= monoèdre) : cette forme ouverte est composée d'un seul plan (face) ;
- Pinacoïde : forme ouverte composée de deux plans (faces) parallèles ;
- Dièdre : forme ouverte composée de deux plans (faces) qui se coupent en une arête commune (un peu comme un toit de maison à deux pentes…) ;
- Prisme rhombique : forme ouverte composée de quatre plans faces) non parallèles ;
- et tous les autres prismes…
- les formes ouvertes - dont les faces ne peuvent pas, à elles seules, former un volume - doivent impérativement s'associer à d'autres formes :
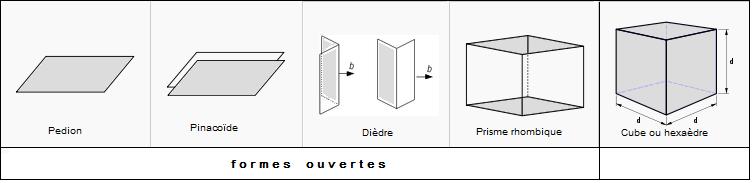
Un cristal ne peut donc pas consister en une seule forme ouverte, tandis qu'il peut développer une seule forme fermée (tel le cube illustré ci-dessus).
La nomenclature officielle française des formes cristallines fut publiée dans : J.D.H. Donnay et H. Curien, « Nomenclature des 47 formes cristallines ».
Classification des 47 formes cristallines :
- Pedion
- Pinacoïde
- Dièdre
- Prisme rhombique
- Pyramide rhombique
- Pyramide trigonale
- Pyramide tétragonale
- Pyramide hexagonale
- Pyramide ditrigonale
- Pyramide ditétragonale
- Pyramide dihexagonale
- Prisme trigonal
- Prisme tétragonal
- Prisme hexagonal
- Prisme ditrigonal
- Prisme ditétragonal
- Prisme dihexagonal
- Disphénoïde rhombique
- Bipyramide rhombique
- Bipyramide trigonale
- Bipyramide tétragonale
- Bipyramide hexagonale
- Bipyramide ditrigonale
- Bipyramide ditétragonale
- Bipyramide dihexagonale
- Disphénoïde tétragonal
- Rhomboèdre
- Scalénoèdre tétragonal
- Scalénoèdre ditrigonal
- Trapézoèdre tétragonal
- Trapézoèdre trigonal
- Trapézoèdre hexagonal
- Tétartoïde ou Pentagonotritétraèdre
- Pentagonododecaèdre
- Diploèdre ou Didodécaèdre
- Gyroïde ou Pentagonotrioctaèdre
- Tétraèdre
- Tétragonotritétraèdre
- Trigonotritétraèdre
- Hexatétraèdre
- Cube ou hexaèdre
- Octaèdre
- Rhombododécaèdre
- Trigonotrioctaèdre
- Tétragonotrioctaèdre
- Tétrahexaèdre
- Hexaoctaèdre
| Minéralogie |
| Vocabulaire géologique | Lexique des termes employés en minéralogie | Lexique volcanologique | Fiches_de_présentation_des_roches |