Cristallographie : Différence entre versions
| Ligne 8 : | Ligne 8 : | ||
**l'holoédrie est la propriété d'un cristal dont la symétrie est exactement celle du réseau périodique qui lui correspond. | **l'holoédrie est la propriété d'un cristal dont la symétrie est exactement celle du réseau périodique qui lui correspond. | ||
**la mériédrie est la propriété d'un cristal dont la symétrie est inférieure à celle du réseau périodique qui lui correspond. Elle est divisée en: | **la mériédrie est la propriété d'un cristal dont la symétrie est inférieure à celle du réseau périodique qui lui correspond. Elle est divisée en: | ||
| − | + | ***hémiédrie, ou mériédrie d'ordre 2 | |
| − | + | ***tétartoédrie, ou mériédrie d'ordre 4 | |
| − | + | ***ogdoédrie, ou mériédrie d'ordre 8 | |
*un polyèdre est une forme géométrique à trois dimensions ayant des faces planes qui se rencontrent le long d'arêtes droites. | *un polyèdre est une forme géométrique à trois dimensions ayant des faces planes qui se rencontrent le long d'arêtes droites. | ||
Version du 1 mai 2009 à 10:23
La cristallographie est la science qui se consacre à l'étude des substances cristallines à l'échelle atomique. Les propriétés physico-chimiques d'un cristal sont étroitement liées à l'arrangement spatial des atomes dans la matière. L'état cristallin est défini par un caractère périodique et ordonné à l'échelle atomique ou moléculaire.
- Termes utilisés en cristallographie:
- trigonale qualifie une forme construite sur une base à 3 côtés.
- tétragonale qualifie une forme construite sur une base à 4 côtés.
- ditrigonale qualifie une forme construite sur une base à 6 côtés.
- holoaxe qualifie un cristal qui possède tous ses axes de symétrie.
- l'holoédrie est la propriété d'un cristal dont la symétrie est exactement celle du réseau périodique qui lui correspond.
- la mériédrie est la propriété d'un cristal dont la symétrie est inférieure à celle du réseau périodique qui lui correspond. Elle est divisée en:
- hémiédrie, ou mériédrie d'ordre 2
- tétartoédrie, ou mériédrie d'ordre 4
- ogdoédrie, ou mériédrie d'ordre 8
- un polyèdre est une forme géométrique à trois dimensions ayant des faces planes qui se rencontrent le long d'arêtes droites.
- Un cuboctaèdre est un polyèdre à 14 faces régulières, dont huit sont des triangles équilatéraux et six sont des carrés.
- un diploèdre est une combinaison de deux rhomboèdres.
- un dodécaèdre est un polyèdre à douze faces dont chacune est un pentagone.
- un hexaèdre est un polyèdre à six faces. Il existe un hexaèdre régulier : le cube.
- un icosaèdre est un polyèdre contenant exactement 20 faces dont chacune est un triangle équilatéral.
- une pinacoïde est une forme « ouverte » délimitée par 2 faces parallèles.
- un octaèdre est un polyèdre à huit faces dont chacune est un triangle équilatéral.
- un rhomboèdre est un parallélépipède dont les faces sont des losanges.
- un scalénoèdre est un polyèdre irrégulier dont les faces forment des triangles dont les trois côtés sont inégaux.
- un tétraèdre est un polyèdre dont les faces sont quatre triangles.
- un trapézoèdre est un solide dont les faces sont des trapèzes.
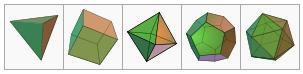
Les cinq polyèdres réguliers convexes (solides de Platon) sont: le tétraèdre, l'hexaèdre(ou cube), l'octaèdre, le dodécaèdre et l'icosaèdre :
en cours !!