Cristallographie : Différence entre versions
| (27 révisions intermédiaires par 3 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
| − | <b>La cristallographie</b> est la science qui se consacre à l'étude des substances cristallines à l'échelle atomique. Les propriétés physico-chimiques d'un cristal sont étroitement liées à l'arrangement spatial des | + | ====Cristallographie==== |
| + | <b>Cristallographie</b> du latin <em>crystallus</em> cristal (objet de cristal, glace, ...), dérivé du grec ancien <em>krystallos</em> glace ; et de <em>graphie</em> écriture.<br> | ||
| + | <b>La cristallographie</b> est la science qui se consacre à l'étude des substances cristallines à l'échelle atomique. Les propriétés physico-chimiques d'un [[cristal]] sont étroitement liées à l'arrangement spatial des [[atome]]s dans la matière. L'état cristallin est défini par un caractère périodique et ordonné à l'échelle atomique ou moléculaire. | ||
| − | C'est en 1774 que l'abbé [[Haüy]] ébauche les premières théories sur l'organisation de la matière. Il décrira les règles géométriques, leur agencement | + | <b>Cristallographe</b> (n. m. ou f.) : Celui ou celle qui s'adonne à l'étude de la cristallographie.<br> |
| + | <b>Cristallographique</b> (adj.) : Qui se rapporte à la cristallographie. | ||
| + | <b>Cristallogénèse</b>(n.f.) c'est la formation d'un cristal, soit en milieu naturel, soit de façon expérimentale. | ||
| + | |||
| + | <b>[[Cristal]]</b>(n.m.) c'est un solide polyédrique.<br> | ||
| + | <b>Cristalliser</b> (verbe) se former en cristal.<br> | ||
| + | <b>Cristallisé (s)</b> (adj.) qui est sous forme de cristal (aux).<br> | ||
| + | <b>Cristallisation</b> (n. f.) action de cristalliser.<br> | ||
| + | <b>Cristallin (e)</b> (adj) relatif au cristal.<br> | ||
| + | <b>Cristallier</b> (n. m.) chercheur de cristaux.<br> | ||
| + | <b>Recristalliser</b> (recristallisation) produire des cristaux différents des cristaux précédents, dans une roche.<br> | ||
| + | |||
| + | =====Historique===== | ||
| + | Les cristaux ont depuis fort longtemps passionné les minéralogistes et collectionneurs.<br>C'est en 1774 que l'abbé [[Haüy]] ébauche les premières théories sur l'organisation de la matière. Il décrira les règles géométriques, leur agencement ; il dégage l'idée d'[[atome]], d'unité et de périodicité à partir de l'observation du phénomène de [[clivage]] d'un cristal de [[calcite]] cassé : les bases de la cristallographie.<br> | ||
<center>[[Image:Hauy_rene_just.jpg]]</center><br> | <center>[[Image:Hauy_rene_just.jpg]]</center><br> | ||
| − | C'est en 1783 que [[Romé de l’Isle | + | C'est en 1783 que [[Romé de l’Isle]] utilisera des notions de description, "[[troncatures]]" et "formes primitives", qui l'amèneront à formuler sa loi de "constance des angles dièdres".<br> |
| − | <center> | + | Gabriel Delafosse, élève de l'abbé René Just Haüy, déduira la notion de [[maille élémentaire]] en 1840.<br> |
| − | [[Image: | + | Auguste [[Bravais]] définit, en 1848, les 14 [[réseaux de Bravais]] à partir des différentes combinaisons des éléments de symétrie cristalline : les 32 classes de symétrie par Johann [[Hessel]] en 1830, liés à 7 types fondamentaux de symétrie d'orientation : les 7 [[systèmes cristallins]] étudiés par Friederich [[Mohs]] en 1820.<br> |
| + | Ces systèmes sont caractérisés par le rapport des longueurs des trois vecteurs et des trois axes, et les valeurs des trois angles que forment entre eux ces axes. [[Les indices de Miller]], système de notation créé en 1839 par William Hallowes [[Miller]], sont les coordonnées des vecteurs dans cette base.<br> | ||
| + | Mais ce n'est qu'au début du XXe siècle, lorsque [[Max Von Laue]] fera diffracter les rayons X sur de la [[halite]], que la structure des cristaux sera vraiment prouvée ; il recevra d'ailleurs le Prix Nobel de Physique pour cette découverte ! Dans les années 1960 l'apparition du [[microscope]] électronique à transmission (MET) permettra de voir réellement les réseaux cristallins ! <center> | ||
| + | [[Image:Rom%C3%A9del%27isle.jpg]] | ||
</center><br> | </center><br> | ||
| − | |||
| − | |||
| − | |||
| − | + | ====Termes utilisés en cristallographie==== | |
| + | *Termes utilisés en cristallographie | ||
| + | **pour les [[forme]]s : | ||
| + | ***trigonale, qualifie une forme construite sur une base à 3 côtés. | ||
| + | ***tétragonale, qualifie une forme construite sur une base à 4 côtés. | ||
| + | ***ditrigonale, qualifie une forme construite sur une base à 6 côtés. | ||
| + | **pour la symétrie : | ||
| + | ***holoaxe, qualifie un cristal qui possède tous ses axes de symétrie. | ||
| + | ***l'holoédrie, est la propriété d'un cristal dont la symétrie est exactement celle du [[réseau périodique]] qui lui correspond. | ||
| + | ***la mériédrie, est la propriété d'un cristal dont la symétrie est inférieure à celle du réseau périodique qui lui correspond. Elle est divisée en : | ||
| + | ****hémiédrie, ou mériédrie d'ordre 2 | ||
| + | ****tétartoédrie, ou mériédrie d'ordre 4 | ||
| + | ****ogdoédrie, ou mériédrie d'ordre 8 | ||
| + | |||
| + | <center>[[Image:Pyramide.jpg]]</center> | ||
| + | =====Formes cristallines===== | ||
| + | On distingue deux sortes de [[forme]]s cristallines : | ||
| + | *les formes ouvertes dont les faces ne peuvent pas former un volume à elles seules, elles doivent impérativement s'associer à d'autres formes : | ||
| + | **<b>Pedion</b> (= monoèdre) : cette forme ouverte est composée d'un seul plan (face) ; | ||
| + | **<b>Pinacoïde</b> : forme ouverte composée de deux plans (faces) parallèles ; | ||
| + | **<b>Dièdre</b> : forme ouverte composée de deux plans (faces) qui se coupent en une arête commune (un peu comme un toit de maison à deux pentes…) ; | ||
| + | **Prisme rhombique : forme ouverte composée de quatre plans (faces) non parallèles ; | ||
| + | **et tous les autres prismes… | ||
| + | *les formes fermées qui sont des volumes à elles seules, aucune face ne manque. Exemples : | ||
| + | **Tétraèdre : forme fermée composée de quatre faces ; | ||
| + | **Cube (ou hexaèdre) : forme fermée composée de six faces carrées ; | ||
| + | **Octaèdre : forme fermée composée de huit faces triangulaires ; | ||
| + | **etc. | ||
| − | *un polyèdre (du | + | <center>[[Image:Formes_ouvertes.jpg]]</center> |
| + | |||
| + | Un cristal ne peut donc pas consister en une seule forme ouverte, tandis qu'il peut développer une seule forme fermée. | ||
| + | |||
| + | *<b>Un [[cristal]]</b> est un solide polyédrique, à structure régulière et périodique, formée d'un ensemble ordonné d'un grand nombre d'atomes, de molécules ou d'ions.<br><center>[[Image:Polyedre.jpg]]</center> | ||
| + | |||
| + | |||
| + | *<b>Un [[polyèdre]]</b> (du grec <em>polus</em>, nombreux, indiquant la pluralité, et <em>hedra</em>, face - base) est une forme géométrique à trois dimensions ayant des faces planes qui se rencontrent le long d'arêtes droites. | ||
**Un cuboctaèdre est un polyèdre à 14 faces régulières, dont huit sont des triangles équilatéraux et six sont des carrés. | **Un cuboctaèdre est un polyèdre à 14 faces régulières, dont huit sont des triangles équilatéraux et six sont des carrés. | ||
| − | ** | + | **Un diploèdre est une combinaison de deux rhomboèdres. |
| − | ** | + | **Un dodécaèdre pentagonal, ou pentagonododécaèdre, est un polyèdre à douze faces, dont chacune est un pentagone. |
| − | ** | + | **Un hexaèdre est un polyèdre à six faces. Il existe un hexaèdre régulier : le cube. |
| − | ** | + | **Un icosaèdre est un polyèdre contenant exactement 20 faces, dont chacune est un triangle équilatéral. |
| − | ** | + | **Un octaèdre est un polyèdre à huit faces, dont chacune est un triangle équilatéral. |
| − | + | **Un rhomboèdre, ou rhombododécaèdre, est un parallélépipède, dont les douze faces sont des losanges égaux. | |
| − | ** | + | **Un scalénoèdre est un polyèdre irrégulier, dont les faces forment des triangles dont les trois côtés sont inégaux. |
| − | ** | + | **Un tétraèdre est un polyèdre dont les faces sont quatre triangles. |
| − | ** | + | **Un trapézoèdre est un solide dont les faces sont des trapèzes. |
| − | ** | ||
<center> | <center> | ||
[[Image:Formes.jpg]] | [[Image:Formes.jpg]] | ||
</center> | </center> | ||
| − | Les cinq polyèdres réguliers convexes (solides de [[Platon]]) sont : le tétraèdre, l'hexaèdre(ou cube), l'octaèdre, le dodécaèdre et l'icosaèdre : | + | Les cinq polyèdres réguliers convexes (solides de [[Platon]]) sont : le tétraèdre, l'hexaèdre (ou cube), l'octaèdre, le dodécaèdre et l'icosaèdre : |
<center> | <center> | ||
[[Image:Solides_de_platon.jpg]] | [[Image:Solides_de_platon.jpg]] | ||
</center> | </center> | ||
| − | + | =====La Cristallographie 2D :===== | |
| − | + | <center> | |
| − | + | [[Image:Loi_de_constance_des_angles.jpg]] | |
| − | + | </center> | |
| − | + | ||
| − | + | Les différents éléments de symétrie et leurs symboles (on notera l'absence d'axe d'ordre 5 dans les minéraux ainsi que d'axes d'ordres supérieurs à 6) : | |
| − | + | ||
| − | + | <center> | |
| − | + | [[Image:Elements_symétrie_cristallo2D.jpg ]] | |
| − | + | </center> | |
| − | + | ||
| − | + | Réseaux et mailles : il est possible de décrire la périodicité par 2 vecteurs de base a et b. La maille sera le plus petit parallélogramme qui suffit à décrire le plan, cette maille est définie par les vecteurs a et b. Le réseau est engendré par la translation de la maille par les vecteurs de base ; tous les noeuds du réseau sont définis par cette translation. | |
| − | < | + | |
| + | <center> | ||
| + | [[Image:la_bonne_maille_2D.jpg]] | ||
| + | </center> | ||
page en cours ... | page en cours ... | ||
| − | <font color="# | + | <hr> |
| + | <font color="#green">Retour à </font>[[Lexique des termes employés en minéralogie]] | ||
<hr> | <hr> | ||
| Ligne 55 : | Ligne 107 : | ||
{| align="center" class="toccolours" cellspacing="0" | {| align="center" class="toccolours" cellspacing="0" | ||
|- bgcolor="#ccccff" | |- bgcolor="#ccccff" | ||
| − | | align="center" | ''' | + | | align="center" | '''à lire également''' |
|- | |- | ||
| align="center" style="font-size: 100%;" | | | align="center" style="font-size: 100%;" | | ||
| Ligne 63 : | Ligne 115 : | ||
{| align="center" class="toccolours" cellspacing="0" | {| align="center" class="toccolours" cellspacing="0" | ||
|- bgcolor="#ccccff" | |- bgcolor="#ccccff" | ||
| − | | align="center" | ''' | + | | align="center" | '''à voir aussi pour tout ce qui concerne les cristaux''' |
|- | |- | ||
| align="center" style="font-size: 100%;" | | | align="center" style="font-size: 100%;" | | ||
[[Les macles]] | [[Cristal]] | [[Systèmes cristallins]] | [[Troncatures]] | [[Les macles]] | [[Cristal]] | [[Systèmes cristallins]] | [[Troncatures]] | ||
|} | |} | ||
Version actuelle datée du 25 janvier 2021 à 22:26
Sommaire
[masquer]Cristallographie
Cristallographie du latin crystallus cristal (objet de cristal, glace, ...), dérivé du grec ancien krystallos glace ; et de graphie écriture.
La cristallographie est la science qui se consacre à l'étude des substances cristallines à l'échelle atomique. Les propriétés physico-chimiques d'un cristal sont étroitement liées à l'arrangement spatial des atomes dans la matière. L'état cristallin est défini par un caractère périodique et ordonné à l'échelle atomique ou moléculaire.
Cristallographe (n. m. ou f.) : Celui ou celle qui s'adonne à l'étude de la cristallographie.
Cristallographique (adj.) : Qui se rapporte à la cristallographie.
Cristallogénèse(n.f.) c'est la formation d'un cristal, soit en milieu naturel, soit de façon expérimentale.
Cristal(n.m.) c'est un solide polyédrique.
Cristalliser (verbe) se former en cristal.
Cristallisé (s) (adj.) qui est sous forme de cristal (aux).
Cristallisation (n. f.) action de cristalliser.
Cristallin (e) (adj) relatif au cristal.
Cristallier (n. m.) chercheur de cristaux.
Recristalliser (recristallisation) produire des cristaux différents des cristaux précédents, dans une roche.
Historique
Les cristaux ont depuis fort longtemps passionné les minéralogistes et collectionneurs.
C'est en 1774 que l'abbé Haüy ébauche les premières théories sur l'organisation de la matière. Il décrira les règles géométriques, leur agencement ; il dégage l'idée d'atome, d'unité et de périodicité à partir de l'observation du phénomène de clivage d'un cristal de calcite cassé : les bases de la cristallographie.

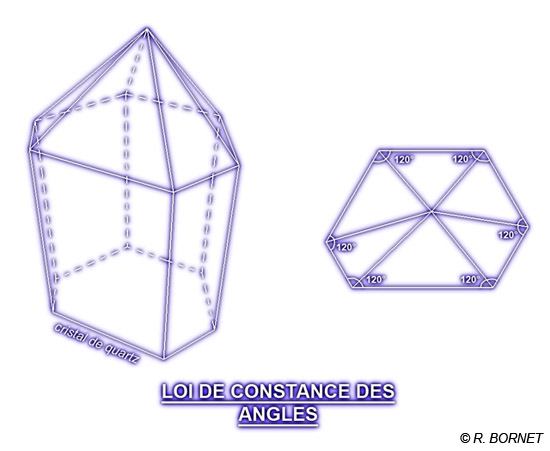
C'est en 1783 que Romé de l’Isle utilisera des notions de description, "troncatures" et "formes primitives", qui l'amèneront à formuler sa loi de "constance des angles dièdres".
Gabriel Delafosse, élève de l'abbé René Just Haüy, déduira la notion de maille élémentaire en 1840.
Auguste Bravais définit, en 1848, les 14 réseaux de Bravais à partir des différentes combinaisons des éléments de symétrie cristalline : les 32 classes de symétrie par Johann Hessel en 1830, liés à 7 types fondamentaux de symétrie d'orientation : les 7 systèmes cristallins étudiés par Friederich Mohs en 1820.
Ces systèmes sont caractérisés par le rapport des longueurs des trois vecteurs et des trois axes, et les valeurs des trois angles que forment entre eux ces axes. Les indices de Miller, système de notation créé en 1839 par William Hallowes Miller, sont les coordonnées des vecteurs dans cette base.
Mais ce n'est qu'au début du XXe siècle, lorsque Max Von Laue fera diffracter les rayons X sur de la halite, que la structure des cristaux sera vraiment prouvée ; il recevra d'ailleurs le Prix Nobel de Physique pour cette découverte ! Dans les années 1960 l'apparition du microscope électronique à transmission (MET) permettra de voir réellement les réseaux cristallins !
Termes utilisés en cristallographie
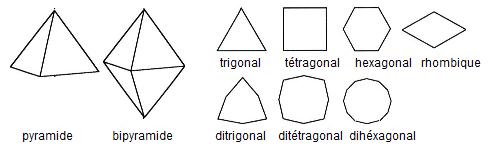
- Termes utilisés en cristallographie
- pour les formes :
- trigonale, qualifie une forme construite sur une base à 3 côtés.
- tétragonale, qualifie une forme construite sur une base à 4 côtés.
- ditrigonale, qualifie une forme construite sur une base à 6 côtés.
- pour la symétrie :
- holoaxe, qualifie un cristal qui possède tous ses axes de symétrie.
- l'holoédrie, est la propriété d'un cristal dont la symétrie est exactement celle du réseau périodique qui lui correspond.
- la mériédrie, est la propriété d'un cristal dont la symétrie est inférieure à celle du réseau périodique qui lui correspond. Elle est divisée en :
- hémiédrie, ou mériédrie d'ordre 2
- tétartoédrie, ou mériédrie d'ordre 4
- ogdoédrie, ou mériédrie d'ordre 8
- pour les formes :
Formes cristallines
On distingue deux sortes de formes cristallines :
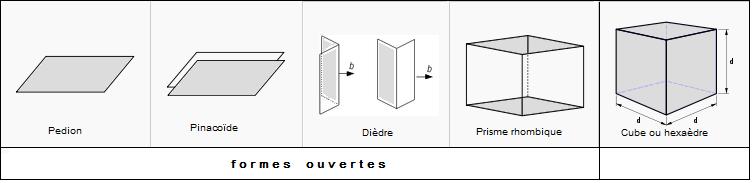
- les formes ouvertes dont les faces ne peuvent pas former un volume à elles seules, elles doivent impérativement s'associer à d'autres formes :
- Pedion (= monoèdre) : cette forme ouverte est composée d'un seul plan (face) ;
- Pinacoïde : forme ouverte composée de deux plans (faces) parallèles ;
- Dièdre : forme ouverte composée de deux plans (faces) qui se coupent en une arête commune (un peu comme un toit de maison à deux pentes…) ;
- Prisme rhombique : forme ouverte composée de quatre plans (faces) non parallèles ;
- et tous les autres prismes…
- les formes fermées qui sont des volumes à elles seules, aucune face ne manque. Exemples :
- Tétraèdre : forme fermée composée de quatre faces ;
- Cube (ou hexaèdre) : forme fermée composée de six faces carrées ;
- Octaèdre : forme fermée composée de huit faces triangulaires ;
- etc.
Un cristal ne peut donc pas consister en une seule forme ouverte, tandis qu'il peut développer une seule forme fermée.
- Un cristal est un solide polyédrique, à structure régulière et périodique, formée d'un ensemble ordonné d'un grand nombre d'atomes, de molécules ou d'ions.
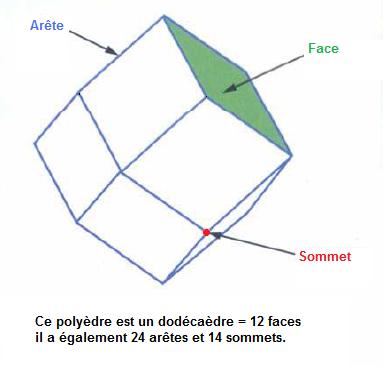
- Un polyèdre (du grec polus, nombreux, indiquant la pluralité, et hedra, face - base) est une forme géométrique à trois dimensions ayant des faces planes qui se rencontrent le long d'arêtes droites.
- Un cuboctaèdre est un polyèdre à 14 faces régulières, dont huit sont des triangles équilatéraux et six sont des carrés.
- Un diploèdre est une combinaison de deux rhomboèdres.
- Un dodécaèdre pentagonal, ou pentagonododécaèdre, est un polyèdre à douze faces, dont chacune est un pentagone.
- Un hexaèdre est un polyèdre à six faces. Il existe un hexaèdre régulier : le cube.
- Un icosaèdre est un polyèdre contenant exactement 20 faces, dont chacune est un triangle équilatéral.
- Un octaèdre est un polyèdre à huit faces, dont chacune est un triangle équilatéral.
- Un rhomboèdre, ou rhombododécaèdre, est un parallélépipède, dont les douze faces sont des losanges égaux.
- Un scalénoèdre est un polyèdre irrégulier, dont les faces forment des triangles dont les trois côtés sont inégaux.
- Un tétraèdre est un polyèdre dont les faces sont quatre triangles.
- Un trapézoèdre est un solide dont les faces sont des trapèzes.
Les cinq polyèdres réguliers convexes (solides de Platon) sont : le tétraèdre, l'hexaèdre (ou cube), l'octaèdre, le dodécaèdre et l'icosaèdre :
La Cristallographie 2D :
Les différents éléments de symétrie et leurs symboles (on notera l'absence d'axe d'ordre 5 dans les minéraux ainsi que d'axes d'ordres supérieurs à 6) :
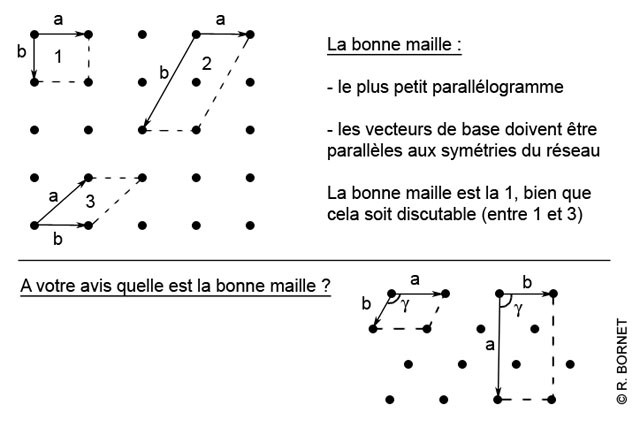
Réseaux et mailles : il est possible de décrire la périodicité par 2 vecteurs de base a et b. La maille sera le plus petit parallélogramme qui suffit à décrire le plan, cette maille est définie par les vecteurs a et b. Le réseau est engendré par la translation de la maille par les vecteurs de base ; tous les noeuds du réseau sont définis par cette translation.
page en cours ...
Retour à Lexique des termes employés en minéralogie
| à lire également |
| à voir aussi pour tout ce qui concerne les cristaux |