Polyèdres : Différence entre versions
(Nouvelle page : *<b>un polyèdre</b> (du grec <em>polus</em>, nombreux, indiquant la pluralité, et <em>hedra</em>, face - base) est une forme géométrique à trois dimensions ayant des faces plane...) |
|||
| (11 révisions intermédiaires par 3 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
| − | *<b>un polyèdre</b> (du grec <em>polus</em>, nombreux, indiquant la pluralité, et <em>hedra</em>, face - base) est une forme géométrique à trois dimensions ayant des faces planes qui se rencontrent le long d'arêtes droites. | + | *<b>un polyèdre</b> (du grec <em>polus</em>, nombreux, indiquant la pluralité, et <em>hedra</em>, face - base) est une forme géométrique à trois dimensions ayant des faces planes qui se rencontrent le long d'arêtes droites.<br>Un polyèdre est construit à partir de différentes sortes d'éléments ou d'entités, chacun associé avec un nombre différent de dimensions : |
| + | **3 dimensions : le corps est limité par les faces, et correspond habituellement au volume compris à l'intérieur. | ||
| + | **2 dimensions : une face est limité par un circuit d'arête, et est habituellement une région plane appelée un polygone. Les faces mises ensemble forment la surface polyédrique. | ||
| + | **1 dimension : une arête joint un sommet à un autre et une face à une autre, et est habituellement une droite d'une certaine sorte. Les arêtes mises ensemble forment le squelette polyédrique. | ||
| + | **0 dimension : un sommet est un point de coin.<br> | ||
| + | <center>[[Image:Polyedre.jpg]]</center> | ||
| + | |||
| + | <b>polyédrique</b> (adj.) Qui est en forme de polyèdre, relatif à un polyèdre.<br> | ||
| + | <b>-ique</b> suffixe utilisé pour la constitution d’un adjectif à partir d’un nom et signifiant "relatif à cette chose, propre à cette chose". Par exemple octaèdrique =en forme d'octaèdre... | ||
| + | |||
| + | *<b>Un [[cristal]]</b> est un solide polyédrique, à structure régulière et périodique, formée d'un ensemble ordonné d'un grand nombre d'[[atome]]s, de molécules ou d'[[ion]]s.<br><center>[[Image:platon.jpg]]<br>exemples de formes polyèdriques de cristaux.</center> | ||
| + | |||
| + | *<b>Quelques polyèdres</b>: | ||
**Un cuboctaèdre est un polyèdre à 14 faces régulières, dont huit sont des triangles équilatéraux et six sont des carrés. | **Un cuboctaèdre est un polyèdre à 14 faces régulières, dont huit sont des triangles équilatéraux et six sont des carrés. | ||
**un diploèdre est une combinaison de deux rhomboèdres. | **un diploèdre est une combinaison de deux rhomboèdres. | ||
| − | **un dodécaèdre est un polyèdre à douze faces dont chacune est un pentagone. | + | **un dodécaèdre pentagonal, ou pentagonododécaèdre, est un polyèdre à douze faces dont chacune est un pentagone. |
**un hexaèdre est un polyèdre à six faces. Il existe un hexaèdre régulier : le cube. | **un hexaèdre est un polyèdre à six faces. Il existe un hexaèdre régulier : le cube. | ||
**un icosaèdre est un polyèdre contenant exactement 20 faces dont chacune est un triangle équilatéral. | **un icosaèdre est un polyèdre contenant exactement 20 faces dont chacune est un triangle équilatéral. | ||
**un octaèdre est un polyèdre à huit faces dont chacune est un triangle équilatéral. | **un octaèdre est un polyèdre à huit faces dont chacune est un triangle équilatéral. | ||
| − | **un rhomboèdre est un parallélépipède dont les faces sont des losanges égaux. | + | **un rhomboèdre, ou rhombododécaèdre, est un parallélépipède dont les douze faces sont des losanges égaux. |
**un scalénoèdre est un polyèdre irrégulier dont les faces forment des triangles dont les trois côtés sont inégaux. | **un scalénoèdre est un polyèdre irrégulier dont les faces forment des triangles dont les trois côtés sont inégaux. | ||
**un tétraèdre est un polyèdre dont les faces sont quatre triangles. | **un tétraèdre est un polyèdre dont les faces sont quatre triangles. | ||
**un trapézoèdre est un solide dont les faces sont des trapèzes. | **un trapézoèdre est un solide dont les faces sont des trapèzes. | ||
<center> | <center> | ||
| + | [[Image:Poly%C3%A8dre.jpg]]<br> | ||
[[Image:Formes.jpg]] | [[Image:Formes.jpg]] | ||
</center> | </center> | ||
| − | + | *<b>Solides de Platon</b>:les cinq polyèdres réguliers convexes (solides de [[Platon]]) sont : le tétraèdre, l'hexaèdre (ou cube), l'octaèdre, le dodécaèdre et l'icosaèdre : | |
<center> | <center> | ||
[[Image:Solides_de_platon.jpg]] | [[Image:Solides_de_platon.jpg]] | ||
</center> | </center> | ||
| + | *<b>Polyèdres en image:</b> | ||
| + | <center> | ||
| + | [[Image:Poly%C3%A8dres_2.jpg]] | ||
| + | [[Image:Poly%C3%A8dres_3.jpg]] | ||
| + | [[Image:Poly%C3%A8dres_4.jpg]] | ||
| + | </center> | ||
| + | *<b>Exemples de minéraux :</b> | ||
| + | <center> | ||
| + | [[Image:Poly%C3%A8dres_exemples.jpg]] | ||
| + | </center><hr> | ||
| + | page en cours ... | ||
| + | |||
| + | <font color="#green">Retour à </font>[[Lexique des termes employés en minéralogie]] | ||
| + | |||
| + | <hr> | ||
| + | <br clear="all" /> | ||
| + | {| align="center" class="toccolours" cellspacing="0" | ||
| + | |- bgcolor="#ccccff" | ||
| + | | align="center" | '''à lire également''' | ||
| + | |- | ||
| + | | align="center" style="font-size: 100%;" | | ||
| + | l'[[Histoire de la minéralogie]] | ||
| + | |} | ||
| + | <br clear="all" /> | ||
| + | {| align="center" class="toccolours" cellspacing="0" | ||
| + | |- bgcolor="#ccccff" | ||
| + | | align="center" | '''à voir aussi pour tout ce qui concerne les cristaux''' | ||
| + | |- | ||
| + | | align="center" style="font-size: 100%;" | | ||
| + | [[Les macles]] | [[Cristal]] | [[Systèmes cristallins]] | [[Troncatures]] | ||
| + | |} | ||
Version actuelle datée du 17 août 2020 à 21:21
- un polyèdre (du grec polus, nombreux, indiquant la pluralité, et hedra, face - base) est une forme géométrique à trois dimensions ayant des faces planes qui se rencontrent le long d'arêtes droites.
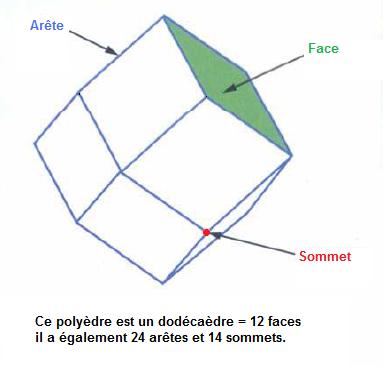
Un polyèdre est construit à partir de différentes sortes d'éléments ou d'entités, chacun associé avec un nombre différent de dimensions :- 3 dimensions : le corps est limité par les faces, et correspond habituellement au volume compris à l'intérieur.
- 2 dimensions : une face est limité par un circuit d'arête, et est habituellement une région plane appelée un polygone. Les faces mises ensemble forment la surface polyédrique.
- 1 dimension : une arête joint un sommet à un autre et une face à une autre, et est habituellement une droite d'une certaine sorte. Les arêtes mises ensemble forment le squelette polyédrique.
- 0 dimension : un sommet est un point de coin.
polyédrique (adj.) Qui est en forme de polyèdre, relatif à un polyèdre.
-ique suffixe utilisé pour la constitution d’un adjectif à partir d’un nom et signifiant "relatif à cette chose, propre à cette chose". Par exemple octaèdrique =en forme d'octaèdre...
- Un cristal est un solide polyédrique, à structure régulière et périodique, formée d'un ensemble ordonné d'un grand nombre d'atomes, de molécules ou d'ions.
exemples de formes polyèdriques de cristaux.
- Quelques polyèdres:
- Un cuboctaèdre est un polyèdre à 14 faces régulières, dont huit sont des triangles équilatéraux et six sont des carrés.
- un diploèdre est une combinaison de deux rhomboèdres.
- un dodécaèdre pentagonal, ou pentagonododécaèdre, est un polyèdre à douze faces dont chacune est un pentagone.
- un hexaèdre est un polyèdre à six faces. Il existe un hexaèdre régulier : le cube.
- un icosaèdre est un polyèdre contenant exactement 20 faces dont chacune est un triangle équilatéral.
- un octaèdre est un polyèdre à huit faces dont chacune est un triangle équilatéral.
- un rhomboèdre, ou rhombododécaèdre, est un parallélépipède dont les douze faces sont des losanges égaux.
- un scalénoèdre est un polyèdre irrégulier dont les faces forment des triangles dont les trois côtés sont inégaux.
- un tétraèdre est un polyèdre dont les faces sont quatre triangles.
- un trapézoèdre est un solide dont les faces sont des trapèzes.
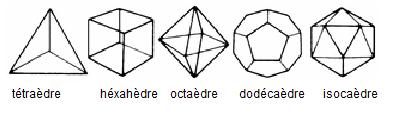
- Solides de Platon:les cinq polyèdres réguliers convexes (solides de Platon) sont : le tétraèdre, l'hexaèdre (ou cube), l'octaèdre, le dodécaèdre et l'icosaèdre :
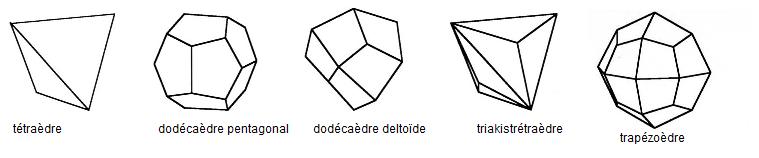
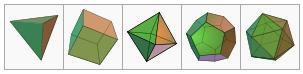
- Polyèdres en image:
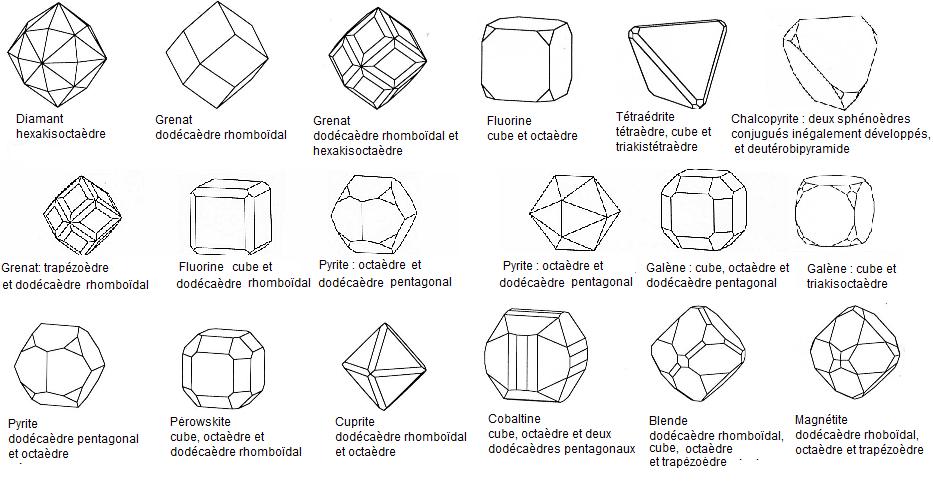
- Exemples de minéraux :
page en cours ...
Retour à Lexique des termes employés en minéralogie
| à lire également |
| à voir aussi pour tout ce qui concerne les cristaux |