Systèmes cristallins : Différence entre versions
m |
|||
| Ligne 6 : | Ligne 6 : | ||
| − | [[Image:Maille | + | ....[[Image:Maille.jpg]] |
| − | [[Image:Cristalo.jpg]] | + | ....[[Image:Cristalo.jpg]] |
| + | |||
| + | ....[[Image:Systcrist.jpg]] | ||
Dans l'énumération qui suit, on donne, le nom du système cristallin, la forme de la maille élémentaire, le rapport des 3 axes (a/b/c), celui des 3 angles (alpha/béta/gamma), entre eux… | Dans l'énumération qui suit, on donne, le nom du système cristallin, la forme de la maille élémentaire, le rapport des 3 axes (a/b/c), celui des 3 angles (alpha/béta/gamma), entre eux… | ||
| Ligne 16 : | Ligne 18 : | ||
cube ; a = b = c ; alpha = béta = gamma = 90° | cube ; a = b = c ; alpha = béta = gamma = 90° | ||
| − | [[Image:Cubique.jpg]][[Image: S_cubique.jpg]] | + | ....[[Image:Cubique.jpg]]..[[Image: S_cubique.jpg]] |
| Ligne 23 : | Ligne 25 : | ||
prisme droit à 4 faces rectangulaires égales et à 2 bases carrées ; a = b ≠ c ; alpha = béta = gamma = 90° | prisme droit à 4 faces rectangulaires égales et à 2 bases carrées ; a = b ≠ c ; alpha = béta = gamma = 90° | ||
| − | [[Image: Quadratique.jpg]][[Image: S_quadra.jpg]] | + | ....[[Image: Quadratique.jpg]]..[[Image: S_quadra.jpg]] |
| Ligne 30 : | Ligne 32 : | ||
prisme droit à 4 faces rectangulaires égales 2 à 2 et à 2 bases rectangulaires ; a ≠ b ≠ c ; alpha = béta = gamma = 90° | prisme droit à 4 faces rectangulaires égales 2 à 2 et à 2 bases rectangulaires ; a ≠ b ≠ c ; alpha = béta = gamma = 90° | ||
| − | [[Image: Orthorhombique.jpg]][[Image: S_orthor.jpg]] | + | ....[[Image: Orthorhombique.jpg]]..[[Image: S_orthor.jpg]] |
| Ligne 37 : | Ligne 39 : | ||
prisme oblique à 4 faces parallélogramatiques égales 2 à 2 et à 2 bases rectangulaires ; a ≠ b ≠ c ; alpha = gamma = 90°, béta ≠ 90° | prisme oblique à 4 faces parallélogramatiques égales 2 à 2 et à 2 bases rectangulaires ; a ≠ b ≠ c ; alpha = gamma = 90°, béta ≠ 90° | ||
| − | [[Image: Monoclinique.jpg]][[Image: S_mono.jpg]] | + | ....[[Image: Monoclinique.jpg]]..[[Image: S_mono.jpg]] |
| Ligne 44 : | Ligne 46 : | ||
prisme oblique à 4 faces latérales et à bases parallélogramatiques égales 2 à 2 ; a ≠ b ≠ c ; alpha ≠ béta ≠ gamma, aucun = 90° | prisme oblique à 4 faces latérales et à bases parallélogramatiques égales 2 à 2 ; a ≠ b ≠ c ; alpha ≠ béta ≠ gamma, aucun = 90° | ||
| − | [[Image: Triclinique.jpg]][[Image: S_triclin.jpg]] | + | ....[[Image: Triclinique.jpg]]..[[Image: S_triclin.jpg]] |
| Ligne 51 : | Ligne 53 : | ||
6 faces losangiques égales (rhomboèdre) ; a = b = c ; alpha = béta = gamma ≠ 90° | 6 faces losangiques égales (rhomboèdre) ; a = b = c ; alpha = béta = gamma ≠ 90° | ||
| − | [[Image: Rhomboedrique.jpg]][[Image: S_rhomboe.jpg]] | + | ....[[Image: Rhomboedrique.jpg]]..[[Image: S_rhomboe.jpg]] |
| Ligne 57 : | Ligne 59 : | ||
prisme droit à 6 faces latérales rectangulaires égales et à 2 bases hexagonales ; a = b ≠ c ; alpha = béta = 90° gamma = 120° | prisme droit à 6 faces latérales rectangulaires égales et à 2 bases hexagonales ; a = b ≠ c ; alpha = béta = 90° gamma = 120° | ||
| − | [[Image:Hexagonale.jpg]][[Image:S_hexa1.jpg]] | + | ....[[Image:Hexagonale.jpg]]..[[Image:S_hexa1.jpg]] |
Version du 7 mars 2009 à 20:53
Sommaire
[masquer]systèmes cristallins
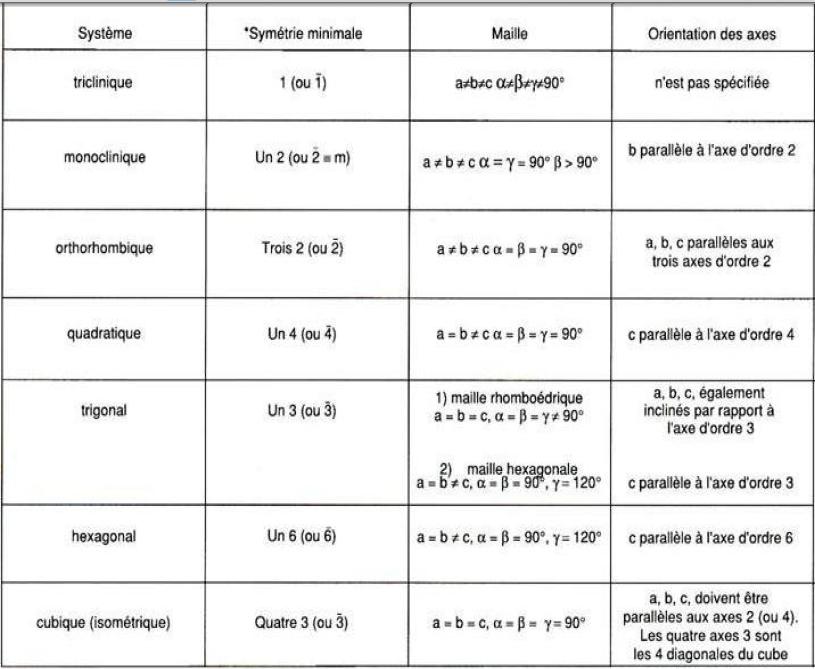
L'étude des cristaux permet de visualiser des plans, axes et centres de symétrie… L'étude des divers éléments de symétrie, a débouché sur la mise en évidence de 14 types de réseaux cristallins (les réseaux " de Bravais "), liés à 7 types fondamentaux de symétrie d'orientation : les 7 systèmes cristallins.
Ces systèmes sont caractérisés par le rapport de 3 axes et des 3 angles que forment entre eux ces axes.
Dans l'énumération qui suit, on donne, le nom du système cristallin, la forme de la maille élémentaire, le rapport des 3 axes (a/b/c), celui des 3 angles (alpha/béta/gamma), entre eux…
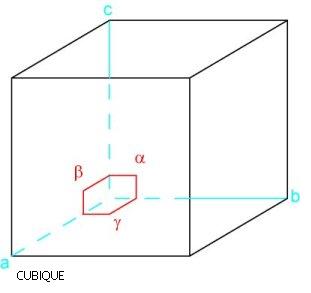
Système cubique
cube ; a = b = c ; alpha = béta = gamma = 90°
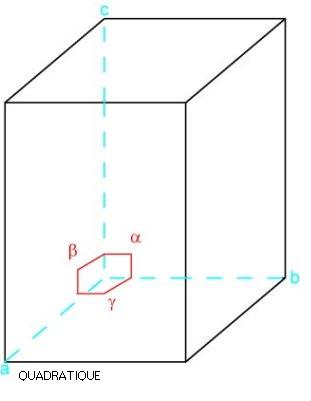
Système quadratique
prisme droit à 4 faces rectangulaires égales et à 2 bases carrées ; a = b ≠ c ; alpha = béta = gamma = 90°
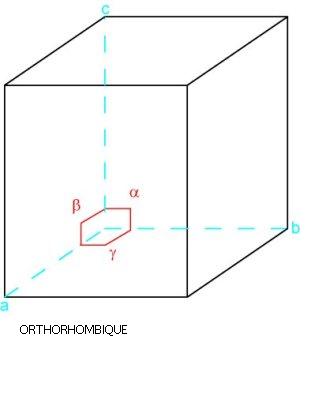
Système orthorhombique
prisme droit à 4 faces rectangulaires égales 2 à 2 et à 2 bases rectangulaires ; a ≠ b ≠ c ; alpha = béta = gamma = 90°
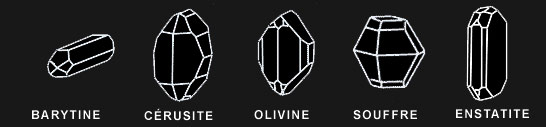
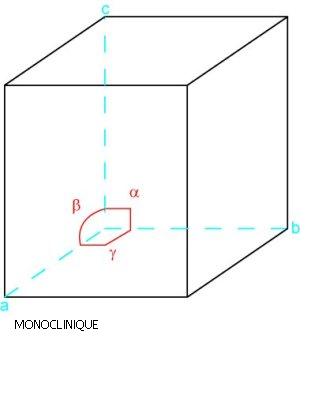
Système monoclinique (ou clinorhombique)
prisme oblique à 4 faces parallélogramatiques égales 2 à 2 et à 2 bases rectangulaires ; a ≠ b ≠ c ; alpha = gamma = 90°, béta ≠ 90°
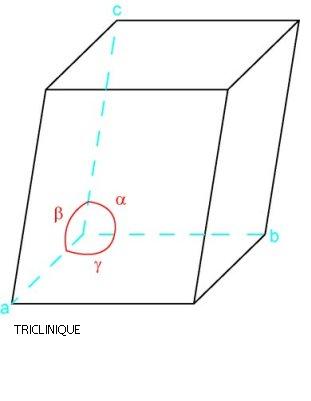
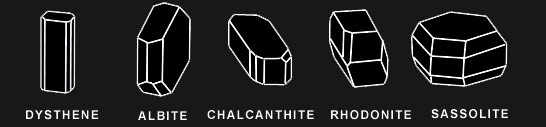
Système triclinique
prisme oblique à 4 faces latérales et à bases parallélogramatiques égales 2 à 2 ; a ≠ b ≠ c ; alpha ≠ béta ≠ gamma, aucun = 90°
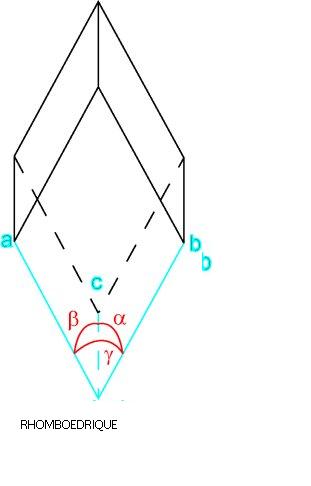
Système trigonal (rhomboédrique ou hexagonal )
6 faces losangiques égales (rhomboèdre) ; a = b = c ; alpha = béta = gamma ≠ 90°
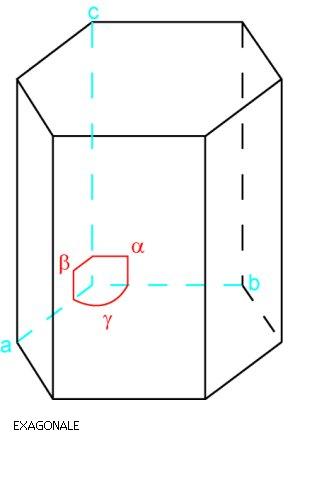
Système hexagonal
prisme droit à 6 faces latérales rectangulaires égales et à 2 bases hexagonales ; a = b ≠ c ; alpha = béta = 90° gamma = 120°