Cristal : Différence entre versions
| Ligne 16 : | Ligne 16 : | ||
<hr> | <hr> | ||
| − | ===<center>La constance des angles=== | + | ===<center>La constance des angles</center>=== |
Les cristaux, pour une espéce donnée, les angles des faces sont égaux quel que soit le dévellopement des faces.<br> | Les cristaux, pour une espéce donnée, les angles des faces sont égaux quel que soit le dévellopement des faces.<br> | ||
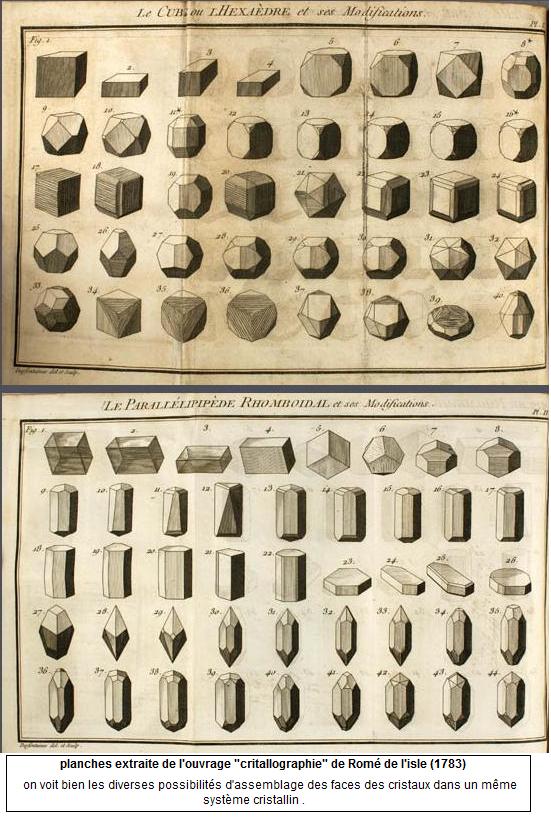
C'est en 1783 que [[Romé de l’Isle | Romé de L'Isle]] utilisera des notions de description "[[troncatures]]" et "formes primitives" qui l'amèneront à formuler sa loi de "constance des angles dièdres". | C'est en 1783 que [[Romé de l’Isle | Romé de L'Isle]] utilisera des notions de description "[[troncatures]]" et "formes primitives" qui l'amèneront à formuler sa loi de "constance des angles dièdres". | ||
| − | + | <center> | |
[[Image:Angles.jpg|159]] | [[Image:Angles.jpg|159]] | ||
</center> | </center> | ||
| Ligne 34 : | Ligne 34 : | ||
<hr> | <hr> | ||
| − | ===La maille élémentaire=== | + | ===<center>La maille élémentaire</center>=== |
| − | + | ||
| − | Gabriel [[Delafosse]], élève de l'abbé René Just [[Haüy]], déduira la notion de maille en 1840. | + | Gabriel [[Delafosse]], élève de l'abbé René Just [[Haüy]], déduira la notion de maille en 1840.<br> |
| − | La maille élémentaire est le plus petit volume cristallin conservant toutes les propriétés physiques, chimiques et géométriques du cristal. Elle est définie par trois vecteurs qui génèrent ainsi six paramètres de mailles : les trois longueurs des vecteurs a, b, c et trois angles α, β, γ, (et trois axes x, y, et z.). | + | La maille élémentaire est le plus petit volume cristallin conservant toutes les propriétés physiques, chimiques et géométriques du cristal. Elle est définie par trois vecteurs qui génèrent ainsi six paramètres de mailles : les trois longueurs des vecteurs a, b, c et trois angles α, β, γ, (et trois axes x, y, et z.).<br> |
Les indices de [[Miller]] sont des coordonnées de vecteurs dans cette base. | Les indices de [[Miller]] sont des coordonnées de vecteurs dans cette base. | ||
| − | + | <center> | |
[[Image:Maille.jpg]] | [[Image:Maille.jpg]] | ||
</center> | </center> | ||
<hr> | <hr> | ||
| − | ===<center>systèmes cristallins=== | + | ===<center>systèmes cristallins</center>=== |
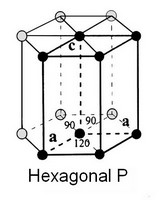
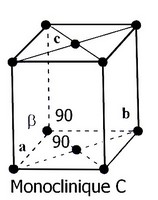
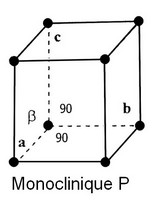
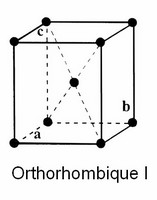
L'étude des cristaux permet de visualiser des plans, axes et centres de symétrie… Auguste [[Bravais]] définit, en 1848, les 14 [[réseaux de Bravais]] à partir des différentes combinaisons des éléments de symétrie cristalline. Les 32 classes de symétrie, définies par Johann [[Hessel]] en 1830, sont liées à 7 types fondamentaux de symétrie d'orientation : les 7 [[systèmes cristallins]] étudiés par Friederich [[Mohs]] en 1820. | L'étude des cristaux permet de visualiser des plans, axes et centres de symétrie… Auguste [[Bravais]] définit, en 1848, les 14 [[réseaux de Bravais]] à partir des différentes combinaisons des éléments de symétrie cristalline. Les 32 classes de symétrie, définies par Johann [[Hessel]] en 1830, sont liées à 7 types fondamentaux de symétrie d'orientation : les 7 [[systèmes cristallins]] étudiés par Friederich [[Mohs]] en 1820. | ||
| − | les 14 [[réseaux de Bravais]] : | + | <center>les 14 [[réseaux de Bravais]] : |
*Système cubique (F, I et P) | *Système cubique (F, I et P) | ||
| Ligne 81 : | Ligne 81 : | ||
*Système trigonal, dit aussi rhomboédrique (R) | *Système trigonal, dit aussi rhomboédrique (R) | ||
| + | </center> | ||
| + | Ces systèmes sont caractérisés par le rapport des longueurs des trois vecteurs "a, b, c," , des trois axes "x, y, z," et des trois angles "α, β, γ," que forment entre eux ces axes ; [[les indices de Miller]] sont des coordonnées des vecteurs dans cette base. | ||
| − | |||
| − | |||
<center> | <center> | ||
| Ligne 90 : | Ligne 90 : | ||
<hr> | <hr> | ||
| − | ===<center>plans et numérotations de Miller=== | + | ===<center>plans et numérotations de Miller</center>=== |
Les [[indice]]s de Miller sont une manière de désigner les divers éléments de géométrie d'un cristal. <br>William Hallowes [[Miller]], en 1839, introduit les notations dites de Miller en cristallographie. | Les [[indice]]s de Miller sont une manière de désigner les divers éléments de géométrie d'un cristal. <br>William Hallowes [[Miller]], en 1839, introduit les notations dites de Miller en cristallographie. | ||
| Ligne 97 : | Ligne 97 : | ||
*Les formes se notent entre accolades {100}. | *Les formes se notent entre accolades {100}. | ||
*Les directions et arêtes se notent entre crochets [001]… | *Les directions et arêtes se notent entre crochets [001]… | ||
| − | + | <center> | |
[[Image:Plans_miller.jpg]] | [[Image:Plans_miller.jpg]] | ||
| Ligne 108 : | Ligne 108 : | ||
Une troncature est le remplacement d'un sommet ou d'une arête d'un cristal par une face plus ou moins importante.<br> | Une troncature est le remplacement d'un sommet ou d'une arête d'un cristal par une face plus ou moins importante.<br> | ||
| − | [[Image:Polyedre.jpg]] | + | [[Image:Polyedre.jpg]]</center> |
Un cristal qui se développe sans contrainte, peut prendre la forme du volume primitif, de l'un des 7 [[systèmes cristallins]]<br> | Un cristal qui se développe sans contrainte, peut prendre la forme du volume primitif, de l'un des 7 [[systèmes cristallins]]<br> | ||
Néanmoins, il a souvent une forme polyédrique plus complexe qui dérive, par [[troncatures]] apparentes, du volume primitif. Une troncature correspond au développement d’une face plane à l’emplacement d’une arête ou d’un sommet du volume primitif, au cours de la croissance du cristal. Lorsque les troncatures sont simples, le cristal conserve l’ensemble des éléments de symétrie du volume primitif. Par exemple, la croissance d’un cristal dont le volume primitif est un cube peut donner un octaèdre. Celui-ci est obtenu par troncatures apparentes des sommets du cube ou des arêtes. L’octaèdre aura les mêmes éléments de symétrie que le cube.<br> | Néanmoins, il a souvent une forme polyédrique plus complexe qui dérive, par [[troncatures]] apparentes, du volume primitif. Une troncature correspond au développement d’une face plane à l’emplacement d’une arête ou d’un sommet du volume primitif, au cours de la croissance du cristal. Lorsque les troncatures sont simples, le cristal conserve l’ensemble des éléments de symétrie du volume primitif. Par exemple, la croissance d’un cristal dont le volume primitif est un cube peut donner un octaèdre. Celui-ci est obtenu par troncatures apparentes des sommets du cube ou des arêtes. L’octaèdre aura les mêmes éléments de symétrie que le cube.<br> | ||
| − | + | ||
<hr> | <hr> | ||
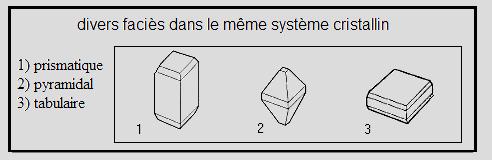
| − | ===<center>Le faciès=== | + | ===<center>Le faciès</center>=== |
Terme général désignant la catégorie dans laquelle on peut ranger un minéral en fonction de ses caractéristiques extérieures. | Terme général désignant la catégorie dans laquelle on peut ranger un minéral en fonction de ses caractéristiques extérieures. | ||
Un même cristal peut présenter des faciès très différents tout en conservant les mêmes angles et faces. | Un même cristal peut présenter des faciès très différents tout en conservant les mêmes angles et faces. | ||
| − | + | <center> | |
[[Image:Faci%C3%A8s.jpg|159]] | [[Image:Faci%C3%A8s.jpg|159]] | ||
| Ligne 132 : | Ligne 132 : | ||
<hr> | <hr> | ||
| − | ===<center>Les habitus=== | + | ===<center>Les habitus</center>=== |
C'est le terme qu'utilisent les minéralogistes pour décrire la forme extérieure d'un minéral. | C'est le terme qu'utilisent les minéralogistes pour décrire la forme extérieure d'un minéral. | ||
| Ligne 150 : | Ligne 150 : | ||
<center> | <center> | ||
[[Image:HABITUS.jpg]] | [[Image:HABITUS.jpg]] | ||
| − | + | </center> | |
On parle également d'habitus pour un même minéral pour justifier l'importance prise par certaines faces du cristal. | On parle également d'habitus pour un même minéral pour justifier l'importance prise par certaines faces du cristal. | ||
Citons, par exemple, quelques habitus du quartz : • habitus du Dauphiné • habitus des Pennines • habitus de Muzo • habitus du Cipo • etc. | Citons, par exemple, quelques habitus du quartz : • habitus du Dauphiné • habitus des Pennines • habitus de Muzo • habitus du Cipo • etc. | ||
| − | + | <center> | |
[[Image:Normal_habit.jpg]][[Image:Trigonal_habit.jpg]][[Image:Pseudohex_habit.jpg]][[Image:Pseudohex_habit.bis.jpg]] | [[Image:Normal_habit.jpg]][[Image:Trigonal_habit.jpg]][[Image:Pseudohex_habit.jpg]][[Image:Pseudohex_habit.bis.jpg]] | ||
| Ligne 161 : | Ligne 161 : | ||
<hr> | <hr> | ||
| − | ===<center>La terminaison=== | + | ===<center>La terminaison</center>=== |
La terminaison c'est la ou les faces de l'extrémité d'un [[cristal]], qui peut être très variable suivant la croissance des dites faces, voir "à habitus". Très souvent, la terminaison d'un cristal est composée de plusieurs faces pouvant appartenir à plusieurs formes cristallines différentes. C'est le cas pour la terminaison de ce cristal de quartz : le prisme hexagonal {10-10} est surmonté par les deux rhomboèdres {10-11} et {01-11} ; entre ces faces de rhomboèdres et celles du prisme, s'intercallent des facettes appartenant à la dipyramide trigonale et au trapézoèdre trigonal (dit également, gyroèdre trigonal. Cette dernière face a son importance : observer sa position, permet de dire si le quartz est dextre ou sénestre…<br> | La terminaison c'est la ou les faces de l'extrémité d'un [[cristal]], qui peut être très variable suivant la croissance des dites faces, voir "à habitus". Très souvent, la terminaison d'un cristal est composée de plusieurs faces pouvant appartenir à plusieurs formes cristallines différentes. C'est le cas pour la terminaison de ce cristal de quartz : le prisme hexagonal {10-10} est surmonté par les deux rhomboèdres {10-11} et {01-11} ; entre ces faces de rhomboèdres et celles du prisme, s'intercallent des facettes appartenant à la dipyramide trigonale et au trapézoèdre trigonal (dit également, gyroèdre trigonal. Cette dernière face a son importance : observer sa position, permet de dire si le quartz est dextre ou sénestre…<br> | ||
| − | [[Image:Terminaison.jpg]]</center> | + | <center>[[Image:Terminaison.jpg]]</center> |
<hr> | <hr> | ||
Version du 13 novembre 2009 à 07:07
Sommaire
[masquer]CRISTAL
Un cristal est un solide polyédrique, à structure régulière et périodique, formée d'un ensemble ordonné d'un grand nombre d'atomes, de molécules ou d'ions. Un minéral est par définition cristallisé. On parle d'un minéral massif quand on ne peut reconnaitre ses formes cristallines.
Le cristal, d’abord simple objet de curiosité, passionna les collectionneurs avant d’intriguer les savants qui, en étudiant sa structure, ébauchèrent les premières théories sur la constitution intime de la matière.
La cristallographie est la science qui se consacre à l'étude des substances cristallines à l'échelle atomique.
Cristalliser (verbe) se former en cristal.
Cristallisé (s) (adj.) qui est sous forme de cristal (aux).
Cristallisation (n. f.) action de cristalliser.
Cristallin (e) (adj) relatif au cristal.
Cristallier (n. m.) chercheur de cristaux.
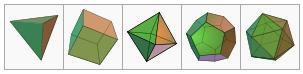
exemples de formes polyèdriques.
La constance des angles
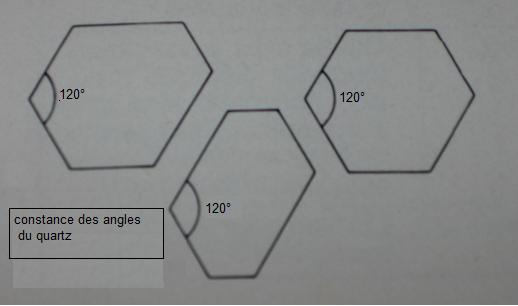
Les cristaux, pour une espéce donnée, les angles des faces sont égaux quel que soit le dévellopement des faces.
C'est en 1783 que Romé de L'Isle utilisera des notions de description "troncatures" et "formes primitives" qui l'amèneront à formuler sa loi de "constance des angles dièdres".
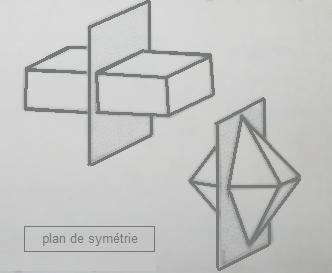
La symétrie
les cristaux présentent une symétrie suivant un plan ou un axe.
La maille élémentaire
Gabriel Delafosse, élève de l'abbé René Just Haüy, déduira la notion de maille en 1840.
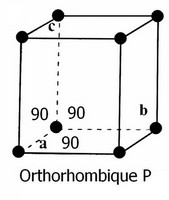
La maille élémentaire est le plus petit volume cristallin conservant toutes les propriétés physiques, chimiques et géométriques du cristal. Elle est définie par trois vecteurs qui génèrent ainsi six paramètres de mailles : les trois longueurs des vecteurs a, b, c et trois angles α, β, γ, (et trois axes x, y, et z.).
Les indices de Miller sont des coordonnées de vecteurs dans cette base.
systèmes cristallins
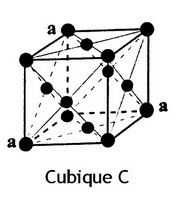
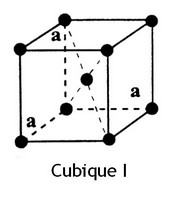
L'étude des cristaux permet de visualiser des plans, axes et centres de symétrie… Auguste Bravais définit, en 1848, les 14 réseaux de Bravais à partir des différentes combinaisons des éléments de symétrie cristalline. Les 32 classes de symétrie, définies par Johann Hessel en 1830, sont liées à 7 types fondamentaux de symétrie d'orientation : les 7 systèmes cristallins étudiés par Friederich Mohs en 1820.
- Système cubique (F, I et P)
- Système hexagonal (P)
- Système monoclinique (C et P)
- Système orthorhombique (C, F, I et P)
- Système tétragonal, dit aussi, quadratique (I et P)
- Système triclinique (P)
- Système trigonal, dit aussi rhomboédrique (R)
Ces systèmes sont caractérisés par le rapport des longueurs des trois vecteurs "a, b, c," , des trois axes "x, y, z," et des trois angles "α, β, γ," que forment entre eux ces axes ; les indices de Miller sont des coordonnées des vecteurs dans cette base.
plans et numérotations de Miller
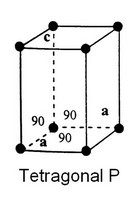
Les indices de Miller sont une manière de désigner les divers éléments de géométrie d'un cristal.
William Hallowes Miller, en 1839, introduit les notations dites de Miller en cristallographie.
- Les faces se notent entre parenthèses : (010) où le premier chiffre est relatif à l'axe a, le deuxième, à l'axe b, le troisième, à l'axe c. (a, b, c peuvent être surmontés d'une petite flèche…).
- Les formes se notent entre accolades {100}.
- Les directions et arêtes se notent entre crochets [001]…
les troncatures
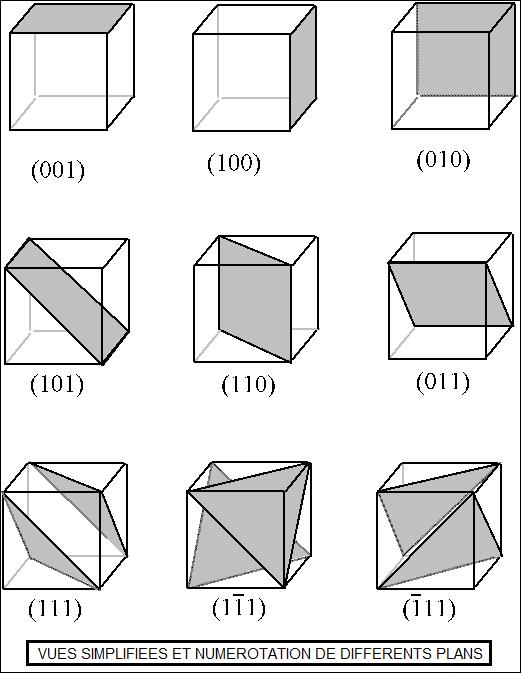
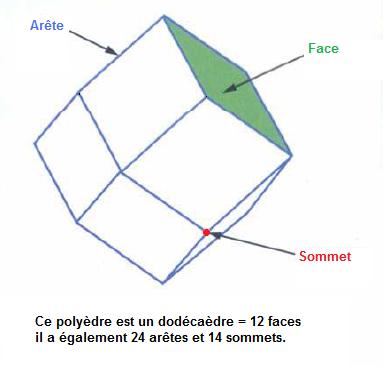
Une troncature est le remplacement d'un sommet ou d'une arête d'un cristal par une face plus ou moins importante.
Un cristal qui se développe sans contrainte, peut prendre la forme du volume primitif, de l'un des 7 systèmes cristallins
Néanmoins, il a souvent une forme polyédrique plus complexe qui dérive, par troncatures apparentes, du volume primitif. Une troncature correspond au développement d’une face plane à l’emplacement d’une arête ou d’un sommet du volume primitif, au cours de la croissance du cristal. Lorsque les troncatures sont simples, le cristal conserve l’ensemble des éléments de symétrie du volume primitif. Par exemple, la croissance d’un cristal dont le volume primitif est un cube peut donner un octaèdre. Celui-ci est obtenu par troncatures apparentes des sommets du cube ou des arêtes. L’octaèdre aura les mêmes éléments de symétrie que le cube.
Le faciès
Terme général désignant la catégorie dans laquelle on peut ranger un minéral en fonction de ses caractéristiques extérieures. Un même cristal peut présenter des faciès très différents tout en conservant les mêmes angles et faces.
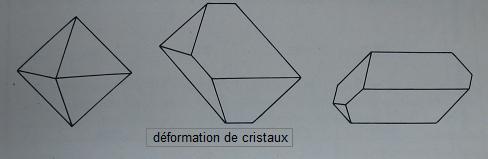
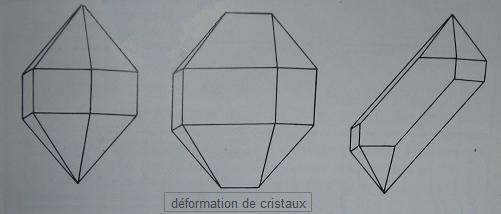
Le faciès peut aussi dépendre de la croissance du cristal et de ses déformations lors de la croissance.
Les habitus
C'est le terme qu'utilisent les minéralogistes pour décrire la forme extérieure d'un minéral. L’habitus décrit les différentes formes, propres à chaque minéral. Pour décrire ces particularités on utilise divers qualificatifs précisant la forme cristalline, un aplatissement ou un allongement. On parle alors d’habitus octaédrique, pyramidal, prismatique ou encore
d’habitus isométrique, allongé, prismatique, aciculaire, tabulaire, etc...
- on distingue plusieurs habitus :
- prismatique : en forme de prismes (ex : quartz, tourmaline, pyromorphite...)
- aciculaire : en forme d'aiguilles (ex : crocoïte, stibine, actinote...)
- capilaire : forme de cheuveux (ex : boulangérite, cyanotrichite, "amiante"...)
- tabulaire en forme de tablettes (ex : barytine, wulfénite, autunite...)
- lamellaire en forme de lamelles (ex : mica, ...)
- isométrique de taille égales dans tout les sens (ex : soufre, pyrite, sphalérite...)
On parle également d'habitus pour un même minéral pour justifier l'importance prise par certaines faces du cristal. Citons, par exemple, quelques habitus du quartz : • habitus du Dauphiné • habitus des Pennines • habitus de Muzo • habitus du Cipo • etc.
La terminaison
La terminaison c'est la ou les faces de l'extrémité d'un cristal, qui peut être très variable suivant la croissance des dites faces, voir "à habitus". Très souvent, la terminaison d'un cristal est composée de plusieurs faces pouvant appartenir à plusieurs formes cristallines différentes. C'est le cas pour la terminaison de ce cristal de quartz : le prisme hexagonal {10-10} est surmonté par les deux rhomboèdres {10-11} et {01-11} ; entre ces faces de rhomboèdres et celles du prisme, s'intercallent des facettes appartenant à la dipyramide trigonale et au trapézoèdre trigonal (dit également, gyroèdre trigonal. Cette dernière face a son importance : observer sa position, permet de dire si le quartz est dextre ou sénestre…
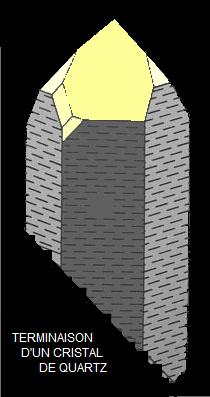
Les agrégats
- Agrégat cristallin: assemblages formés de cristaux.
- Aciculaire : agrégat de cristaux en forme d'aiguilles (exemples : actinote, stibine).
- Bacillaire : agrégat de cristaux allongés en forme de baguettes (exemples : tourmaline, aragonite).
- Botryoïdal : agrégat de cristaux en forme de grappe (exemple : calcédoine).
- Capillaire : agrégat de cristaux très allongés et très fins (exemple : rutile).
- Compact : agrégat massif de minéraux non distingables individuellement.
- Concrétionné : agrégat de minéraux disposés en forme de couches concentriques (exemple : malachite).
- Ecailleux : agrégat de cristaux aplatis pouvant se détacher en écailles.
- Fibreux : agrégat de cristaux allongés en forme de fibres (exemple: " amiante ").
- Granulaire : agrégat de minéraux en forme de grains sensiblement isométriques.
- Lamellaire : agrégat de minéraux en forme de lames minces.
- Laminaire : agrégat de minéraux en forme de lames assez grandes et épaisses (exemple : gypse).
- Micacé : agrégat de minéraux aplatis en forme de lames très minces et larges (exemple : muscovite).
- Pulvérulent : Texture caractérisant des masses de minéraux en grains très fins, faiblement agrégés.
- Radié : agrégat de cristaux allongés et rayonnants (exemple : wavellite).
- autres formes : termes souvent utilisées pour décrire les "agrégats"
- Coralloïde : minéraux en forme de corail (branches ramifiées).
- Globulaire : minéraux en forme de portions de sphères.
- Nodulaire : minéraux présentant une forme extérieure en forme de tubercules (nodules).
- Oolithique : minéraux en forme de sphères d'un diamètre allant de 0,5 à 2 mm.
- Pisolitique : minéraux en forme de sphères parfaites, de pois, de diamètre supérieur à 2 mm.
- Stalactitique : minéraux disposés en colonnes, semblables aux stalactites (exemple : calcédoine).
Retour à Lexique des termes employés en minéralogie
| Géologie |
|
Les macles | systèmes cristallins | La cristallographie | Troncatures |